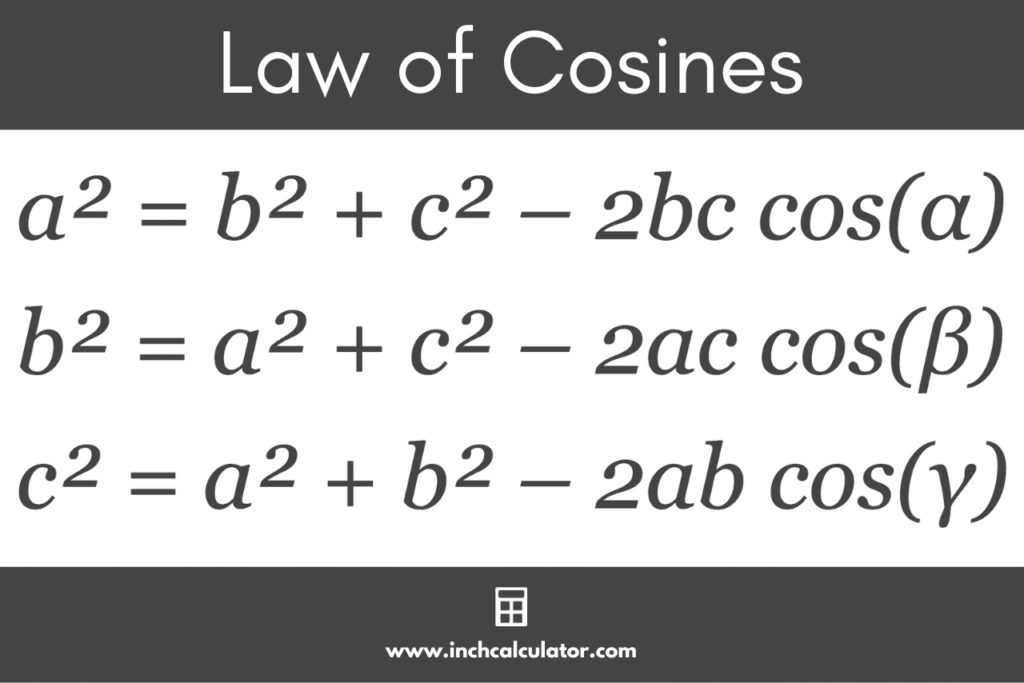The cosine rule, also known as the law of cosines, is one of the most fundamental principles in trigonometry, connecting the lengths of a triangle’s sides with the cosine of their angles. This comprehensive article covers its definition, origin, usage, controversies, life cycle, applications, breed (variants), recent news, FAQs, and every crucial detail.
What is the Cosine Rule?
The cosine rule expresses a direct relationship between the sides and angles of any triangle. If a triangle has sides a, b, and c opposite the angles α, β, and γ, respectively, the rule states:
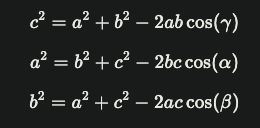
The cosine rule noticeably generalises the Pythagorean theorem, which only applies to right triangles. When the angle is 90°, cos(90°)=0, so the rule reduces to c2=a2+b2.
Life Cycle and Evolution of Cosine Rule
The origins of the cosine rule reach back to ancient Greek mathematics. The geometric roots were established by Euclid in his work “Elements” around 300 BCE, describing relationships structurally equivalent to today’s cosine rule, but without modern trigonometric notation. The true birth of the squared cosine law, as known today, occurred in the 15th century when Persian mathematician Jamshīd al-Kāshī formally expressed and used it in triangulation. French mathematicians later named it “Le théorème d’Al-Kashi” to honour his work.
Over centuries, the cosine rule moved from geometry to trigonometry, becoming a mainstay in applications like navigation, astronomy, engineering, and more.
“Breed”, Variants of the Cosine Rule
- Standard Law of Cosines: For flat, planar triangles, as described above.
- Spherical Law of Cosines: Used for triangles drawn on the surface of a sphere, crucial in geodesy and navigation.
For spherical triangles:cos(c)=cos(a)cos(b)+sin(a)sin(b)cos(C) - Extensions: Used in vector mathematics and computer graphics, adapting the rule for higher dimensions.
Applications and Practical Usage
The cosine rule solves triangles when three sides are known or two sides and the included angle are known. It’s invaluable in fields such as:
- Surveying and navigation are used to find distances and bearings.
- Astronomy is used for calculating spatial angles between celestial objects.
- Engineering, in resolving forces or measurements.
- Computer graphics is used for modelling transformations and shapes.
- Education is where it forms part of the core curriculum worldwide.
Origin and Historical Significance
From Euclid’s geometrical compositions to Jamshīd al-Kāshī’s analytic trigonometry, the cosine rule’s history features intellectual milestones:
- Euclid (300 BCE): Described geometric equivalence in his “Elements”.
- al-Kāshī (15th century): Explicitly stated the cosine rule, used for calculation in astronomy and navigation.
- Europe (17th-19th centuries): The adoption and integration of cosine and other trigonometric functions facilitated their broader use in science and engineering.
Controversies Associated with the Cosine Rule
While not controversial in theory, disputes have arisen regarding its historical attribution:
- Naming debate: Credit for the discovery of the cosine rule has sparked discussion among historians, with French, Persian, and Greek mathematicians all given recognition at different times.
- Pedagogy: In recent years, there have been debates about how much trigonometry, including the cosine rule, should be taught in schools, especially as digital tools automate solutions.
- Computational accuracy: In practical applications, such as GPS systems, minor misinterpretations of spherical forms led to significant real-world errors, prompting research into improved formulas for curved surfaces.
Recent News and Developments
- 2025 Curriculum Updates: Major educational boards have announced revisions to trigonometry modules, emphasising the practical applications and historical context of the cosine rule.
- Tech Advances: AI-based navigation systems now implement advanced forms of the law, allowing for better real-time mapping and resource location.
- International Math Competitions: The role of the cosine rule in problem-solving remains central, as reflected by breakthroughs in competitive mathematics throughout 2025.
FAQs About Cosine Rule
What is the cosine rule used for?
The cosine rule is used to calculate unknown sides or angles in any triangle where conventional methods like the Pythagorean theorem do not apply, especially for non-right triangles.
Who discovered the cosine rule?
The geometric principles date to ancient Greece (Euclid), but Jamshīd al-Kāshī in the 15th century is credited with their trigonometric formulation.
How does the cosine rule relate to the Pythagorean theorem?
The cosine rule generalises the Pythagorean theorem. For right triangles, the cosine of 90° is zero, and the rule simplifies to the original theorem’s form.
Can the cosine rule be used for spherical triangles?
Yes, the spherical law of cosines extends the principle to the geometry of a sphere, vital for navigation and astronomy applications.
Is the cosine rule still taught in modern schools?
Yes, it is a foundational topic in mathematics curricula worldwide, with expanded emphasis on applications in science, technology, and engineering.
What are practical examples of using the cosine rule?
It is used in navigation (finding distances), surveying (mapmaking), computer graphics (shape transformations), and astronomy (measuring angles between celestial objects).
What are the mathematical formulas for the cosine rule?
The standard formulas for the law of cosines are:
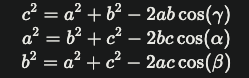
Every Detail at a Glance
- Definition: Relates triangle side lengths to the cosine of their included angles.
- Formula: Three key expressions based on which side and angle are known.
- History: Euclid’s geometry, Jamshīd al-Kāshī’s trigonometry.
- Variants: Standard and spherical forms, plus computer graphics adaptations.
- Applications: Navigation, astronomy, engineering, graphics, and education.
- Controversies: Historical attribution, pedagogical debates, and computational accuracy.
- Recent News: Curriculum updates, tech developments, and competitive mathematics spotlighted in 2025.